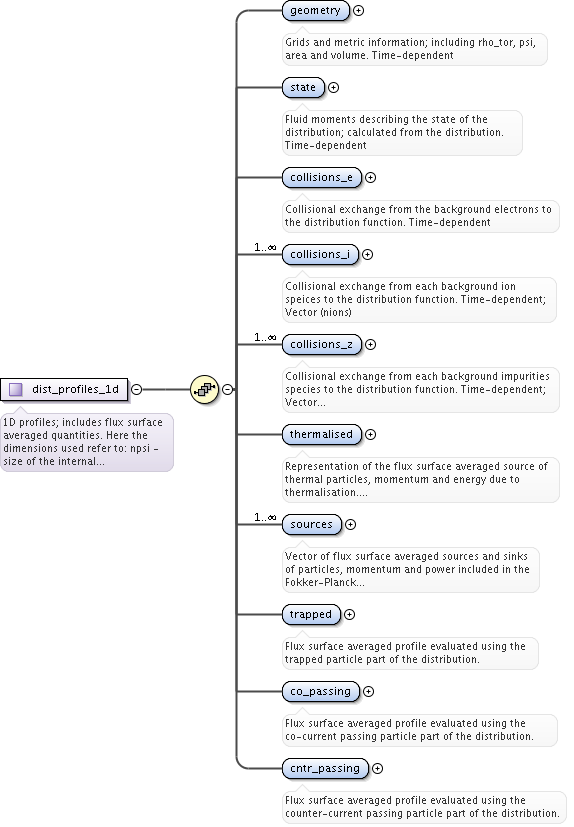
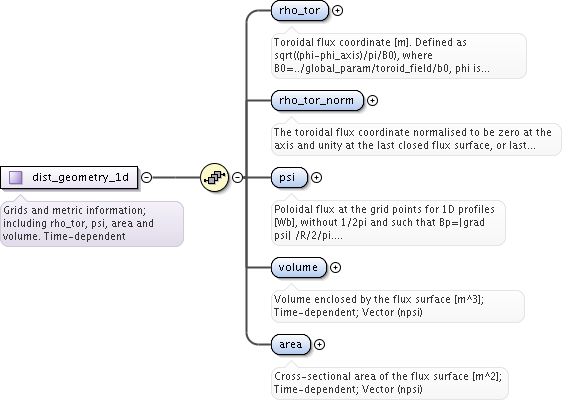
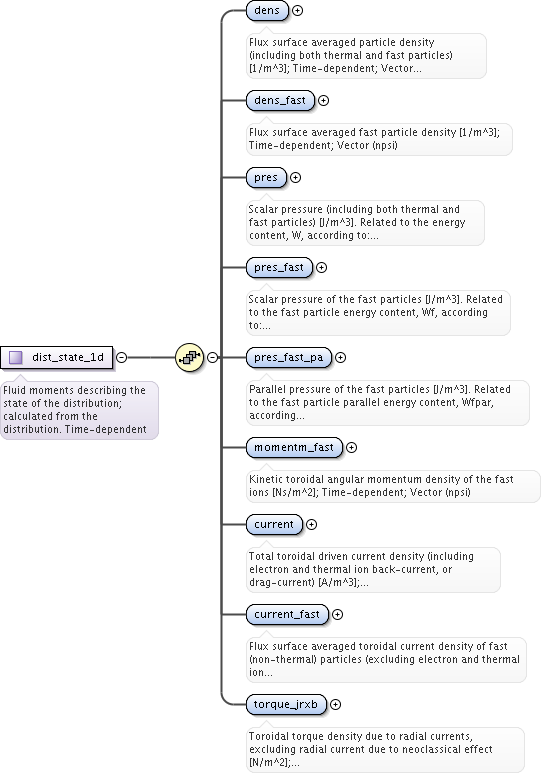
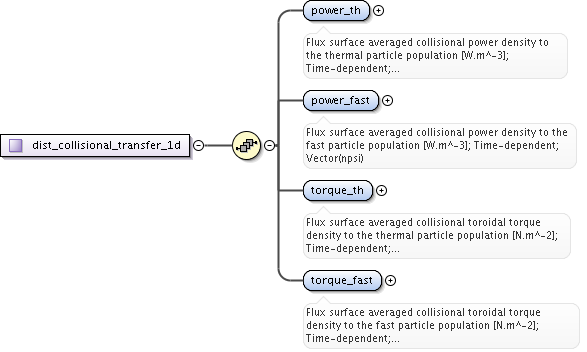
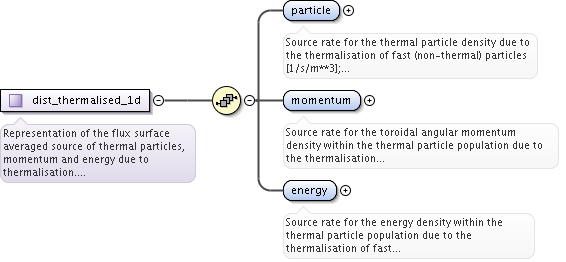
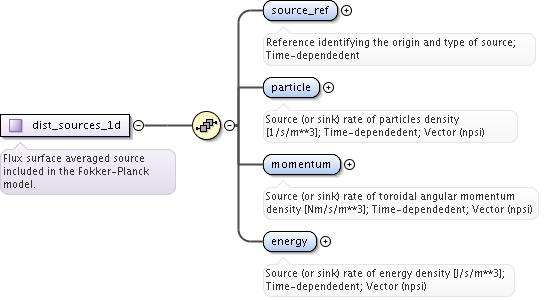
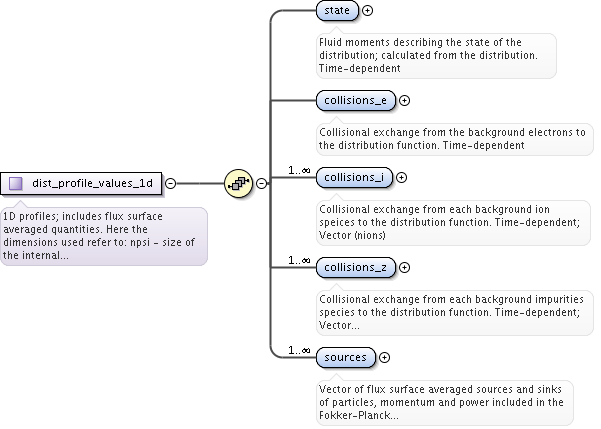
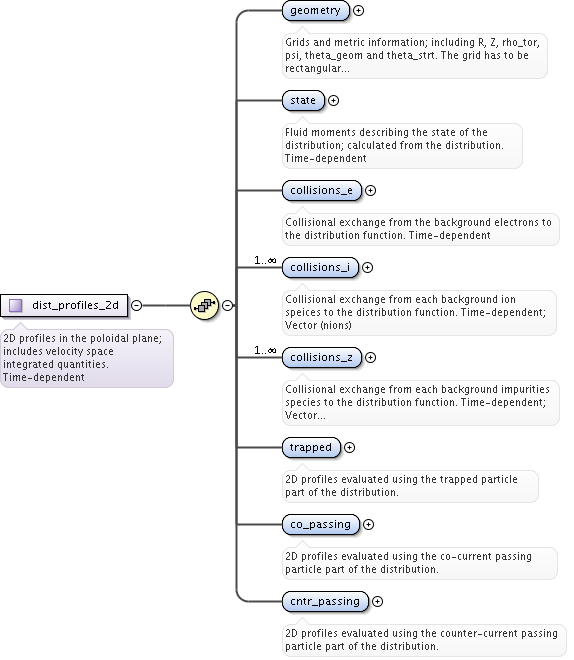
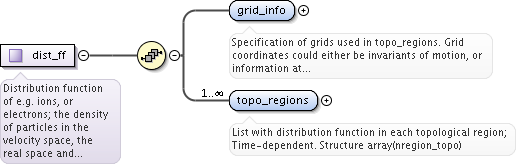
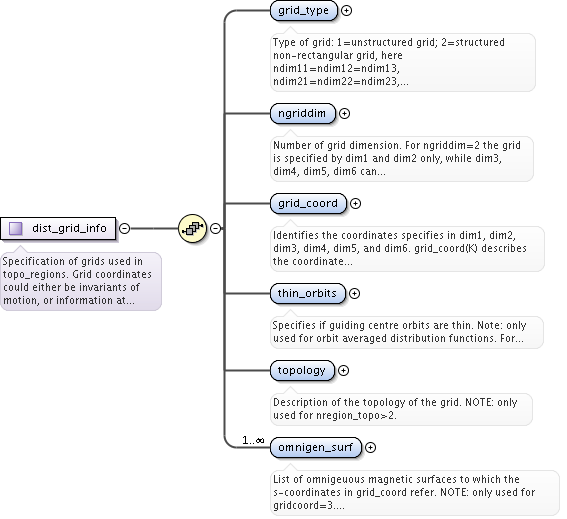
<xs:complexType name="dist_grid_info">
<xs:annotation>
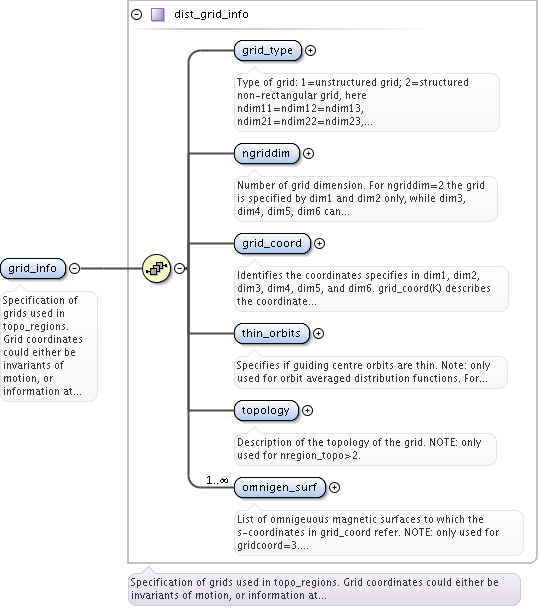
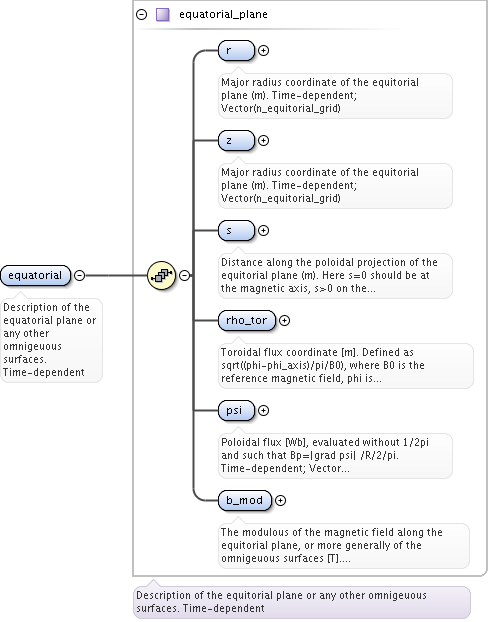
<xs:documentation>Specification of grids used in topo_regions. Grid coordinates could either be invariants of motion, or information at single point along orbit, e.g. xi and s for grid_coord=3. This point should always be on a so-called omnigenous surface (a generalised equitorial plane); grad(psi) x grad(B) = 0. All closed orbits cross omnigenous surfaces at least two times. The omnigenous surfaces are described in omnigen_surf.</xs:documentation>
</xs:annotation>
<xs:sequence>
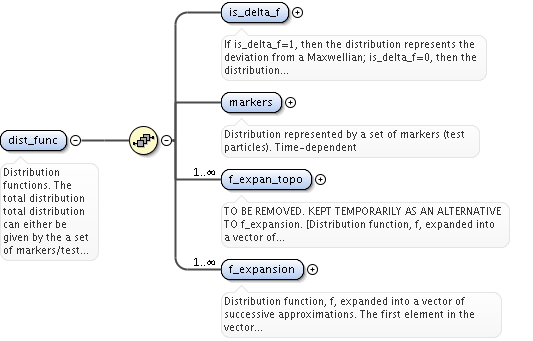
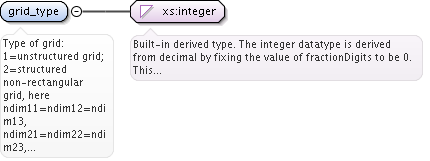
<xs:element name="grid_type" type="xs:integer">
<xs:annotation>
<xs:documentation>Type of grid: 1=unstructured grid; 2=structured non-rectangular grid, here ndim11=ndim12=ndim13, ndim21=ndim22=ndim23, ndim31=ndim32=ndim33; 3=rectangular grid, where grid coordinates are stored in the vectors dim1(1:ndim1,1,1), dim2(1,1:ndim2,1), dim3(1,1,1:ndim3)</xs:documentation>
</xs:annotation>
</xs:element>
<xs:element name="ngriddim" type="xs:integer">
<xs:annotation>
<xs:documentation>Number of grid dimension. For ngriddim=2 the grid is specified by dim1 and dim2 only, while dim3, dim4, dim5, dim6 can be ignored (should not be allocated). For ngriddim=3 also dim3 is used to describe the grid etc. E.g. if your distribution is given by the three variables the poloidal flux, perpendicular and parallel velocities, then ngriddim=3 and grid_coord(1)=15, grid_coord(1)=16, grid_coord(3)=6.</xs:documentation>
</xs:annotation>
</xs:element>
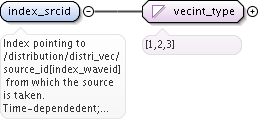
<xs:element name="grid_coord" type="vecint_type">
<xs:annotation>
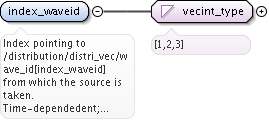
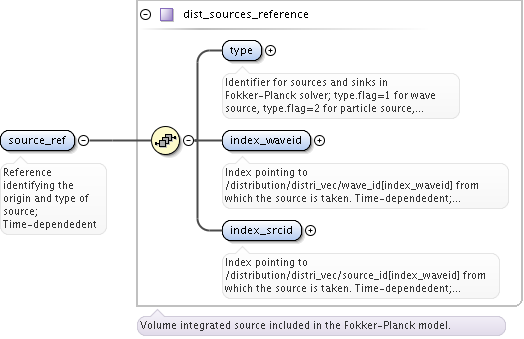
<xs:documentation>Identifies the coordinates specifies in dim1, dim2, dim3, dim4, dim5, and dim6. grid_coord(K) describes the coordinate representaed in dimK, for K=1,2...6. The possible coordinates are: 1=R, Major radius [m]; 2=Z, Vertical position [m]; 3=X, first cartesian coordinate in the horizontal plane [m]; 4=Y, second cartesian coordinate in the horizontal plane (grad(X) x grad(Y) = grad(Z)) [m]; 5=phi, toroidal angle [rad]; 6=psi, poloidal magnetic flux [T*m^2]; 7=rhotor, the square root of the toroidal flux; 8=theta, geometrical poloidal angle [rad]; 9=theta_b, Boozer poloidal angle [rad]; 10=vx, velocity in the x-direction [m/s]; 11=vy, velocity in the y-direction [m/s]; 12=vz, velocity in the z-direction [m/s]; 13=vel, total velocity [m/s]; 14=vphi, velocity in the phi-direction [m/s]; 15=vpar, velocity in the parallel direction [m/s]; 16=vperp, velocity in the perpendicular direction [m/s]; 17=E, Hamiltonian energy [J]; 18=Pphi, canonical toroidal angular momentum [kg m^2/s]; 19=mu, magnetic moment [J/T]; 20=Lambda=mu/E [1/T]; 21=pitch=vpar/v [-]; 22=s, the position of the omnigenous plane (generalised equitorial plane) as described by the fields omnigen_surf%s and omnigen_surf%rz; 23=particle spin; 24=n_Legendre, the index of the Legendre polynomial of the pitch, e.g. if the k:th component of dim3(1,1,k,1,1,1)=5 then this refer to the 5:th Legendre polynomial P_5(xi). Vector (6)</xs:documentation>
</xs:annotation>
</xs:element>
<xs:element name="thin_orbits" type="xs:integer">
<xs:annotation>
<xs:documentation>Specifies if guiding centre orbits are thin. Note: only used for orbit averaged distribution functions. For thin_orbits=1 the orbit are considered thin, i.e. each orbit is bound to follow a single flux surface; for thin_orbits=0 the orbits are asumed to follow guiding centre trajectories. E.g. thin_orbits=0 using constants of motion as given in a generalised equitorial plane, then the orbit outside the equitorial plane are described by the guiding centre equations of motion.</xs:documentation>
</xs:annotation>
</xs:element>
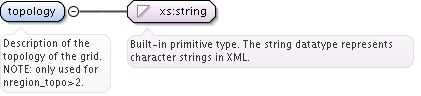
<xs:element name="topology" type="xs:string">
<xs:annotation>
<xs:documentation>Description of the topology of the grid. NOTE: only used for nregion_topo>2.</xs:documentation>
</xs:annotation>
</xs:element>
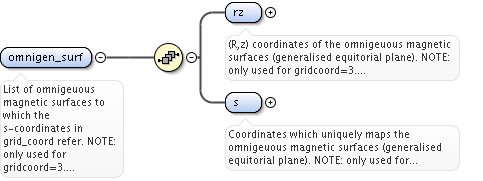
<xs:element name="omnigen_surf" maxOccurs="unbounded">
<xs:annotation>
<xs:documentation>List of omnigeuous magnetic surfaces to which the s-coordinates in grid_coord refer. NOTE: only used for gridcoord=3. NOTE: all guiding centre orbits intersect at least one omnigeuous (or stagnation) surfaces, i.e. the omnigeuous generalised the equitorial plane (the midplane). nsurfs=Number of omnigenous surfaces. Structure array(nregion_topo)</xs:documentation>
</xs:annotation>
<xs:complexType>
<xs:sequence>
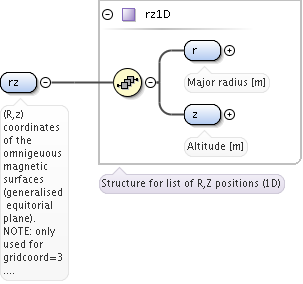
<xs:element name="rz" type="rz1D">
<xs:annotation>
<xs:documentation>(R,z) coordinates of the omnigeuous magnetic surfaces (generalised equitorial plane). NOTE: only used for gridcoord=3. Vector rz1d (nsurfs)</xs:documentation>
</xs:annotation>
</xs:element>
<xs:element name="s" type="vecflt_type">
<xs:annotation>
<xs:documentation>Coordinates which uniquely maps the omnigeuous magnetic surfaces (generalised equitorial plane). NOTE: only used for gridcoord=3. Vector (nsurfs)</xs:documentation>
</xs:annotation>
</xs:element>
</xs:sequence>
</xs:complexType>
</xs:element>
</xs:sequence>
</xs:complexType> |